Lab 1 - Tiger Language

Setup

Before starting this lab, please create a new directory lab1/ in your git repository. Execute the following commands at the top of your repository:

$ mkdir lab1
$ cd lab1
$ wget -qO- www.sifflez.org/lectures/compil/lab1/dragon-tiger.tar.gz | tar zxv
$ git add dragon-tiger
$ git commit -m "Import dragon-tiger for lab1" dragon-tiger
$ cd dragon-tiger

To compile tiger language you need,

• a Tiger compiler called dtiger (inside src/driver/)
• a runtime library libruntime.a (inside src/runtime/posix) that implements all the Tiger primitives such as print or print_int.

You can use dtiger to compile a Tiger program test.tig as follows,

$ echo 'print("Hello World!\n")' > test.tig
$ src/driver/dtiger -o test.o test.tig
$ clang++-9 test.o src/runtime/posix/libruntime.a -o test
$ ./test
Hello World!

The second command transforms the Tiger source into an object file which contains the generated assembly code.

The third command links the object file with the runtime library which contains the implementation of Tiger primitives.

Each time you answer a question marked with [file.ext] you will create a new file lab1/dragon-tiger/file.ext and write the answer inside (a tiger program or a regular expression).

You will then add this new file to the git, commit your changes with a meaningful message and push your changes.

Ensure that you commit everything and follow precisely the instructions. This lab is graded and machine corrected !

Tiger Language

We will familiarize ourselves with the Tiger language by writing a few programs. If in doubt check the specifications of the Tiger language but remember that in these lectures we will not use and implement array and record types.

▶ [hello.tig] Write a Tiger program, hello.tig, that prints the string “Hello World!” followed by a new line character to the standard output.

▶ [fibonacci.tig] Complete the following program and save it in a fibonacci.tig file. The function fibonacci should return the \(n^{th}\) term of the Fibonacci sequence which is defined recursively as follows,

let
   function fibonacci(n : int) : int =
     /* ... complete here ... */
in
   for i := 1 to 8 do
     (print_int(fibonacci(i)); print("\n"))
end

▶ [read_unsigned.tig] Complete the following program and save it in read_unsigned.tig file. The function read_unsigned reads a line from the standard input (stdin). If the line contains only numerical characters it returns the number as a positive base-ten integer. Otherwise, it returns \(-1\). You should correctly handle the line termination character \n.

The following primitives will be useful:

• function getchar() : string, reads a single character from stdin and returns it as string of size one. If EOF is reached, the empty string is returned.
• function ord(s : string) : int, returns the ASCII code of the first character of the input string.

let
  /* Read a positive integer from the standard input.
     Returns -1 on error */
  function read_unsigned() : int =
    /* ... complete here ... */
  var a : int := read_unsigned()
in
  print_int(a*2);
  print("\n")
end

Regular Expressions and Finite Automata

▶ Give a regular expression and an automata for each of the following languages in \(\Sigma = \{a, b\}\):

• [regexp1.txt] words in \(\Sigma^{*}\) for which the first a (if it exist) precedes the first b (if it exists).

• [regexp2.txt] words in \(\Sigma^{*}\) for which the number of a is even (0 is considered even).

You will write regular expressions in the format accepted by grep -E. The two committed files will contain nothing but the regular expression. You can test what a regular expression matches like this:

echo "aaaaab" | grep -E -x --color "$(cat regexp2.txt)"

The parts of the input that match will be colored.

Automata Determinisation

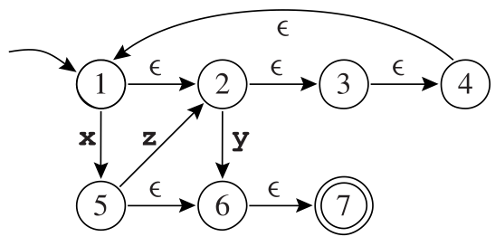
▶ What is the language accepted by the automaton in the figure below?

▶ Show that it is not deterministic.

▶ Determinise it.